In general, the coriolis flow meter manufacturer is stating their accuracy as a total of their base accuracy, zero stability, operating pressure effect, etc. We must carefully calculate their ‘true’ or total accuracy based on information given in their catalogue rather than just use base accuracy as their accuracy.
The accuracy words itself is also ambiguously used by the manufacturer to present their equipment inaccuracy or uncertainty. Thus from now on we will call the accuracy as uncertainty.
How to Calculate Coriolis flow meter uncertainty?
Basically we can express the total uncertainty of the equipment from its individual component uncertainty as below:
Ux = ((c1*Ux1)^2 + (c2*Ux2)^2 + … + (cn*Uxn)^2)^0.5
Where cn is a sensitivity coefficient and Uxn is a standard uncertainty of its individual component and Ux is a total standard uncertainty.
Let’s take an example of how to calculate the coriolis flow meter uncertainty (inaccuracy) as below.
Coriolis Flow Meter Maximum Flow (liquid application) = 3200 lb/min
Calibration Pressure = 30 psig
Calibration Temperature = 25 C
Process Operating Temperature = 41.67 C
Process Operating Pressure = 250 psig
The uncertainty statement from vendor catalogue:
Base accuracy = 0.1% of flow rate
Zero stability = 0.08 lb/min
Operating temperature effect = 0.0005% of the max flow rate per 1°C
Operating pressure effect = 0.0008% of the flow rate per psi
Then we can get the coriolis flow meter uncertainty budget for the maximum flow as below:

Total Standard Uncertainty = (total (c*u)^2)^0.5 = 0.101%
Total Expanded Uncertainty (95% confidence) = 2*standard uncertainty = 0.202% of mass flow rate.
By using the same method as above maximum flow, we can get also the uncertainty budget for the 0.8 flow, 0.6 flow, etc down to 0.01 flow. The uncertainty of the coriolis flow meter will be as per below graph.
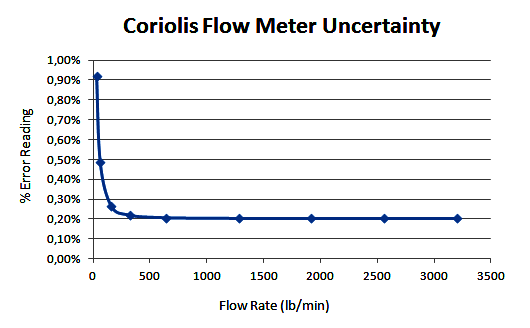
As a conclusion, in general applications the coriolis flow meter may be used for liquid application that require flow measurement uncertainty up to 0.3% of mass flow rate in the 1:20 turndown ratio, 0.5% of mass flow rate in the 1:50 turndown ratio, and 1% of mass flow rate in the 1:100 turndown ratio.
Coriolis flow meter also can be used for gas application that require flow measurement uncertainty up to 1% of mass flow rate in the 1:10 turndown ratio, and 2% of mass flow rate in the 1:20 turndown ratio (see note 5, the uncertainty budget has been done but didn’t shown up in this article for simplicity).
Notes:
The individual expanded uncertainty is calculated from the formula given by the vendor above. For example, from the above data the expanded uncertainty of the operating temperature effect will be 0.0005% *3200 lb/min*(41.67-25) = 0.267 lb/min or in term of flow rate it will be 0.267/3200 % = 0.01%.
The standard uncertainty is the expanded uncertainty divided by 3 if the confidence level is 99% and divided by 2 if the confidence level is 95%. If the vendor didn’t state clearly their confidence level then we can consider as 95% confidence level for most application.
The sensitivity coefficient is considered as 1 since there is no any statement from the vendor regarding the sensitivity coefficient of its individual contributor of uncertainty. This assumption is correct for most coriolis flow meter except the vendor state its sensitivity coefficient.
The vendor information regarding their accuracy may be different from what was calculated here as this is just an example and typical one. One should consider all conditions that may be included in vendor information but didn’t include in this calculation.
From the vendor catalogue, it is stated that the coriolis flow meter uncertainty is bigger in the gas applications since gas is having less density rather than liquid. Gas flow will have a higher fluid velocity rather than liquid flow for the same mass flow rate.
References :
- Measurement of fluid flow – procedure for the evaluation of uncertainties, ISO 5168 2005.
- Instrument Engineer Handbook Volume 1, Process Measurement and Analysis. By Bela G. Liptak (Editor).


